使用Scratch演示如何求最大公约数

有两个自然数a和b，如果a能被b整除，那么，b就叫做a的约数。

两个或多个自然数的共有约数中最大的一个，叫做它们的最大公约数，也称最大公因数、最大公因数。

求最大公约数有多种方法，常见的有质因数分解法、短除法、辗转相除法、辗转相减法、更相减损法等。

【问题】

输入两个正整数x和y，求它们的最大公约数。

【编程解题】

下面我们使用辗转相除法求出两个数的最大公约数。

辗转相除法

辗转相除法的算法步骤：给定两个正整数x、y（x>y），用x除以y等到余数z。如果余数z不为0就将y和z构成新的一组数（x=y，y=z），继续上的除法操作，直到余数z为0，这时y就是原来两个正整数的最大公约数。

由于这个算法需要反复执行除法运算，所以被形象地命名为“辗转相除法”。

举例说明，用辗转相除法求255,75的最大公约数。

给定两个数：255,75

第一次：用255除以75，余数30；

第二次：用75除以30，余数15；

第三次：用30除以15，余数0；

这个时候我们得出255和75的最大公约数是15.

Scratch编程实现算法：

根据上面的算法步骤，我们编写一个名为“辗转相除法”的模块，用来求两个数的最大公约数。该模块的完成代码如下：

下面编写调用“辗转相除法”模块的主程序，用来求255和75的最大公约数。主程序代码如下：

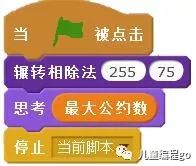
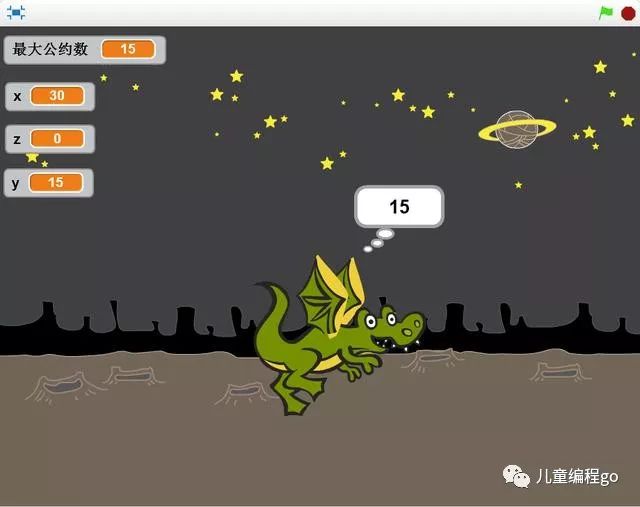
点击小绿旗运行程序，求得255和75的最大公约数是15。